Teilchenmodell
Elektronenmodell
Die Geometrie des Wellenfeldes in der Feldraummechanik verleiht dem Teilchenmodell eine mächtige Modellierungsplattform für beliebig komplexe Hohlkörperschwingungen. Subatomare Strukturen werden als ein Produkt aus Oberwellen berechnet. Jede Oberwelle beschreibt also einen Teil der geometrischen Gesamtanordnung eines Teilchens. Dieser Anteil wird Quarkanregungsfrequenz genannt, und nur durch ihre Kombination entstehen die vielfältigen Teilchenstrukturen, die zum Teil durch Experimente ermittelt und nun vorhergesagt werden können. Die Teilchenmappe fasst verschiedene bekannte und neu vorhergesagte Teilchen zusammen. Es nutzt dabei die Generalformal zur Ermittlung jedlicher Teilchenanregungsfrequenzen. Diese Formel sorgt unter anderem dafür, dass zwischen elektrischer, starker und schwacher Wechselwirkung unterschieden werden kann.
Aus dem Photonenmodell ist bekannt, dass unsichtbare Photonen orthogonal zur Dimensionabene D56 ausgeformt sind. Nur diese sind für eine Teilchenstruktur interessant. Sobald diese eine minimale Kopplungsfrequenz überwunden haben, koppeln diese an einen quantisierten Bereich, welcher Sphäre S genannt wird. Solche unsichtbaren Photonen werden Fionen genannt. Je nach Energieinhalt innerhalb der Sphäre S können sich Bündel aus diesen rotierenden Fionen ausbilden. Mit ihrer orthogonalen Ausformung zur Dimensionsebene D56 generieren diese Teilchen parallel zum elektrischen Potentials des Universums über ihren Rotationsweg eine Ladung im Wellenfeld. Der Feldaustausch mit dem Teilchenfeld findet am Berührungspunkt in der Dimensionsebene D56 statt. Je nach Geometrie und Komplexität wird im Teilchenfeld ein anderer Impuls wahrgenommen und durch die Wechselwirkungskräfte unterschieden.
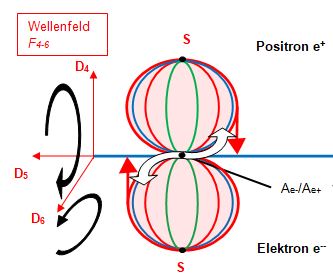
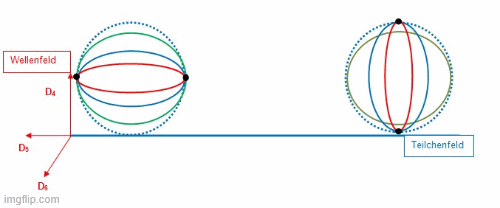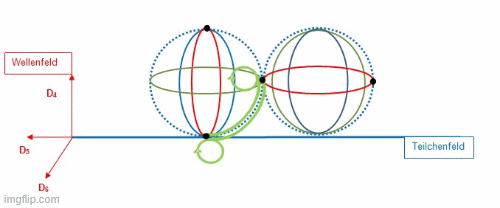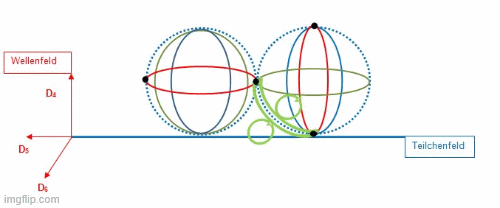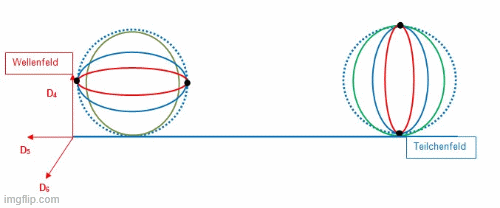
Für das Positron ist in der nachfolgenden Abbildung dargestellt, wie dieses Bündel aus Fionen in Form eines Positrons innerhalb der Sphäre rotiert. Links ist die Geometrie zu erkennen, welche das Positron innerhalb des Teilchenfeldes registrierbar macht. Rechts daneben liegt dasselbe Positron von seinem Berührungspunkt zum Teilchenfeld auf der Dimensionsebene D56 angehoben vor, was zu einem verborgenen (dunkle Materie) Positron führt.
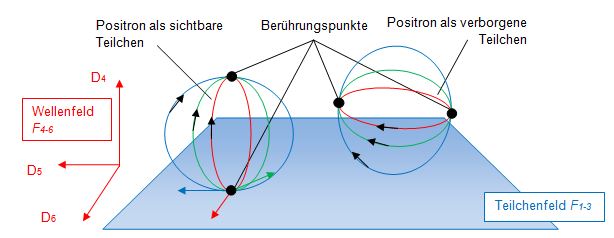
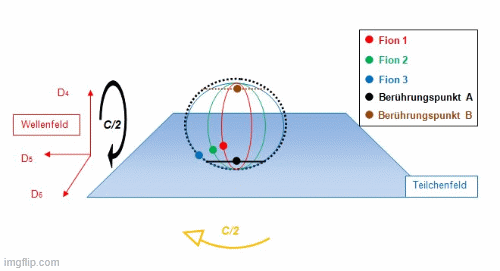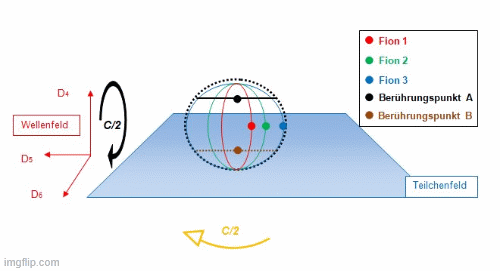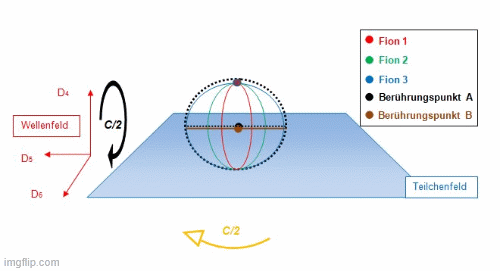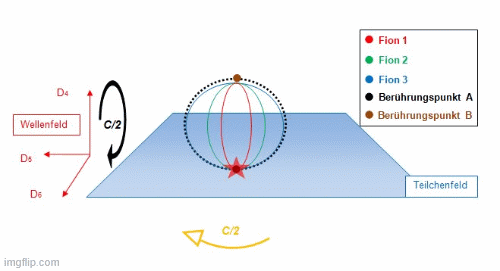
Die Simulation zeigt das dynamische Raumzeitverhalten des Positrons. Entsprechend äquivalent gilt dies für das Elektron, welches unterhalb der Dimensionsebene D56 angeordnet ist. Das Bündel wechselt alle Periode T die Richtung, weil die Sphäre ihre eigene relativistische Dynamik in der Raumzeit einnimmt, um ein Feld zu schaffen, welches aus einer „ruhenden“ elektromagnetischen Hohlkörperschwingung hervorgeht. Mit dieser komplexen Dynamik entsteht am Berührungspunkt das maximale Feld, welches in das Teilchenfeld vermittelt wird. Der rote Stern zeigt nach einer Periode von 2T den Moment dieses Feldaustausches, dass alle Fionen an diesem Berührungspunkt synchron mit der Sphäre ankommen. Die Rotation des Teilchens und jedes Fions läuft mit der halben Maximalgeschwindigkeit c/2 ab. Mit dieser Geometrie werden Drehimpuls, resultierende Rotationsgeschwindigkeiten, Iso-Spins, das Pauli-Prinzip und damit die Wechselwirkung von Feldern und Kopplungsmöglichkeiten zwischen Teilchen erklärbar.
Simulation:
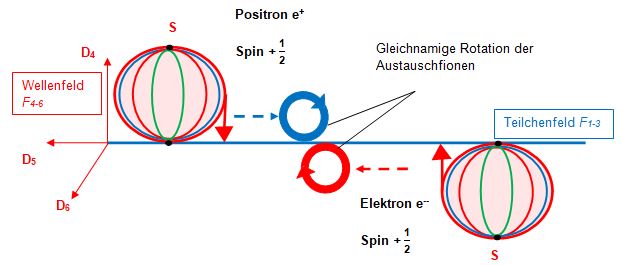
Anziehung zwischen Ladungen
Ungleichnamig geladene Teilchen ziehen einander an, wenn
a) ihre Austauschfionen in gleicher Rotationsrichtung rotieren und mit dem jeweiligen Empfängerteilchen verschmelzen können sowie
b) die aktiven Fionen beider Teilchen in derselben Richtung oberhalb und unterhalb der Dimensionsebene D56 rotieren.
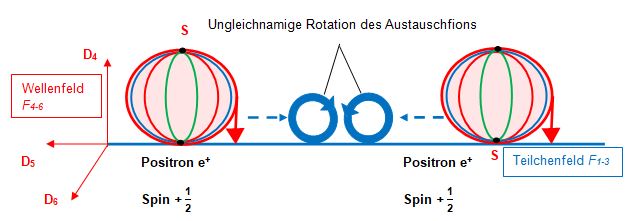
Abstoßung zwischen Ladungen
Gleichnamig geladene Teilchen stoßen einander ab, wenn
c) die Austauschfionen unterschiedlich rotieren und sich somit gegenseitig ignorieren sowie
d) die aktiven Fionen mit ihren Unterräumen in der Sphäre S in gleicher Richtung rotieren.
Vernichtungsreaktion zwischen Ladungen
Eine Vernichtungsreaktion benötigt eine bestimmte raumstrukturelle Beschaffenheit zwischen zwei unterschiedlich geladenen Teilchen.
e) Die aktiven Fionen aus einem Elektron rotieren unterhalb und die aktiven Fionen eines Positrons oberhalb der Dimensionsebene D56,
f) die Rotation ihrer Sphären S findet zur Dimensionsebene D46 antiparallel statt,
g) diese beiden Teilchen kommen sich zu nahe und treffen sich an ihrem jeweiligen Berührungspunkt so, dass ihre Fionen exakt oder nahezu phasengleich am jeweiligen Berührungspunkt gegenüberstehen.
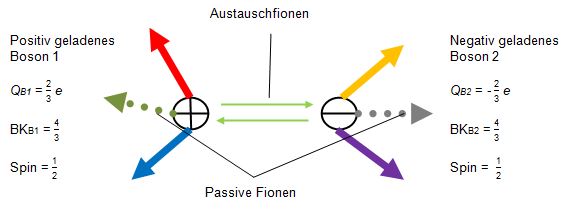
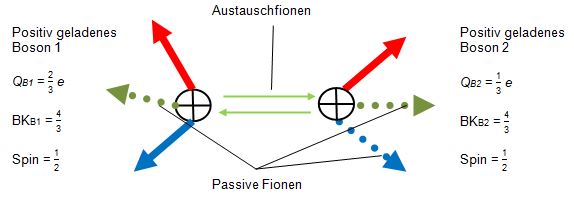
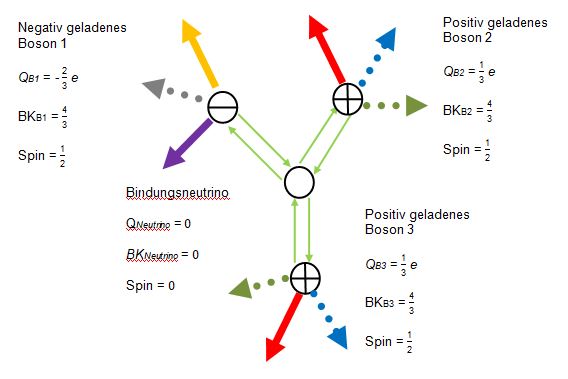
Mesonen bestehen aus zwei Bosonen, welche ihrerseits aus einem Quark und einem Austauschfion bestehen. Die Quarks liefern ein Fion aus ihrem Bündel, um ein Austauschfion herzustellen. Je nach Wechselwirkung mit anderen Teilchen, kann die Gesamtladung von 3/3 auf 2/3 oder gar auf 1/3 abfallen. Das Austauschfion rotiert außerhalb des Bosons mit der Maximalgeschwindigkeit c. Die zu überwindende Entfernung hängt davon ab, wie lang ein Fion rotieren muss, damit sich beim aufnehmenden Boson alle seine Fionen und seine Sphäre S synchron am Berührungspunkt befinden. Nachdem es von dem einen zum anderen Meson hinübergewandert ist, tauscht sich sein Feld während der Rekombinationsphase in das Boson mit dem Teilchenfeld aus. Der Impuls mit seinem Feld wird am Berührungspunkt in der Dimensionsebene D56 vermittelt. Es werden die starke Wechselwirkung und eine Masse im Teilchenfeld registriert.
Simulation:

Simulation:
Simulation:

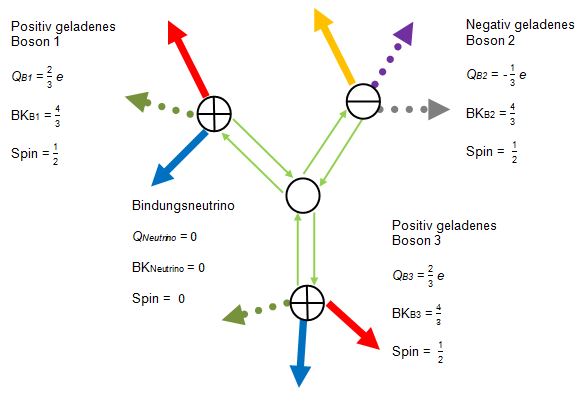
Teilchenstruktur von Mesonen und Baryonen
Teilchen-Austauschfion-Teilchen-Kopplung
Die Teilchen-Austauschfion-Teilchen-Kopplung modelliert jede Teilchenkomplexität, die in irgendeiner Weise in eine Wechselwirkung mündet. Es werden dabei die geometrischen Bedingungen und Wechselwirkungen berücksichtigt, die eine relativistische Rotation in der Raumzeit vollzieht. Aufgrund der komplexen Geometrie beschränkt sich die Generalformel auf das Zählen von Strukturen. Genauere Informationen zur Anwendung stehen im Dokument.

- fObj – Kopplungsfrequenz für beliebige Objekte
- MObj – Masse für beliebige Objekte
- 1/2 – für die halbe Geschwindigkeit eines gebundenen zu einem ungebundenen Austauschfion bei einer Teilchen-Austauschfion-Teilchen-Kopplung
- BK – Bosonenkonfiguration
- KK – Kopplungskonfiguration
- Potenz mit drei für die drei möglichen Fionen, die aus dem Teilchenfeld gestört werden können
- n – n-te Dimensionsfamilie
- TK – Teilchenkonfiguration
- Dimfaktor zur Reduzierung der Maximalgeschwindigkeit c
- Me – Masse des Elektrons
- fe – Frequenz des Elektrons
BK - Bosonenkonfiguration
BK zählt im Zähler alle Fionen im Bündel und zusätzlich zeitlich begrenzt empfangene Fionen in der Sphäre S. Im Nenner wird die maximal mögliche Anzahl von Fionen im Bündel gezählt.
KK - Kopplungskonfiguration
KK fasst im Zähler die maximal mögliche Anzahl von Fionen im Bündel zusammen. Im Nenner steht hingegen die Anzahl der benötigten Perioden T, um eine Synchronisation zwischen Bündelfionen und der Sphäre S zu erzeugen.
TK - Teilchenkonfiguration
TK – beschreibt die gängigen Teilchenarten wie Mesonen, Baryonen, das Elektron oder das freie Fion. Im Zähler werden die Fionen im Bündel zuzüglich extern empfangener Fionen abzüglich aller benötigten Fionen zur Herstellung der geforderten Austauschenfionen gezählt. Im Nenner bleibt die maximale Anzahl der Bündelfionen stehen.
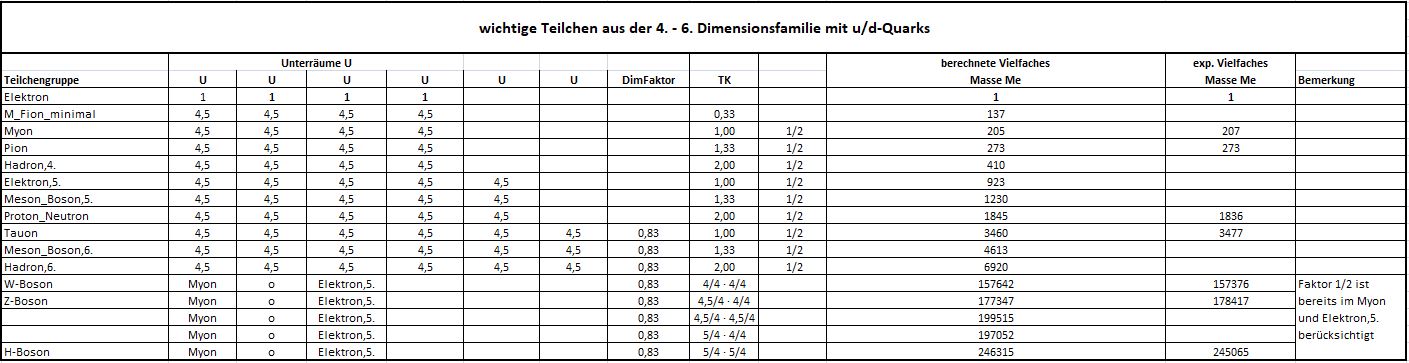
Auszug aus der Teilchenmappe
Nachfolgend werden ausgewählte Teilchen vorgestellt, die in Experimenten gemessen werden. Wenn der Mittelwert ohne Berücksichtigung der Standardabweichungen aus den Experimenten mit dem theoretisch berechneten Wert verglichen wird, dann entsteht zwischen diesen lediglich eine durchschnittliche Abweichung von 1 %. Quelle ist das Particle Data Group (PDG).
Masse Myon
Masse Pion
Masse Proton/Neutron